BAB 3
A. Relasi
Aturan yang menghubungkan setiap anggota himpunan A ke B disebut Relasi dari A ke B.
Di tulis : R : A→B.
Istilah-istilah :
Himpunan A disebut Domain = Daerah Asal
Himpunan B disebut Kodomain = Daerah Kawan
Range = Daerah Hasil
B. Menyatakan Relasi
Relasi dapat dinyatakan dengan tiga cara, yaitu :
1. Diagram Panah
2. Himpunan Pasangan Berurutan
3. Grafik Cartesius
C. Produk Cartesius
Jika x ϵ A dan y ϵ B, maka produk Cartesius A ke B adalah himpunan pasangan berurutan (x, y).
Ditulis : AxB ={(x, y)І xϵ A dan yϵ B}
Contoh :
A = {a, b, c}
B = {1, 2}
maka dengan menggunakan tabel A x B di peroleh :
A x B
|
1
|
2
|
a
|
(a, 1)
|
(a, 2)
|
b
|
(b, 1)
|
(b, 2)
|
c
|
(c, 1)
|
(c, 2)
|
A x B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}
Sifat-sifat :
1. A x B ≠ B x A
2. n(A x B) = n(B x A)
D. Pemetaan (Fungsi)
Pemetaan adalah relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat pada satu anggota himpunan B.
Pemetaan adalah relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat pada satu anggota himpunan B.
Komposisi Fungsi
Komposisi fungsi merupakan penggabungan operasi dua fungsi secara berurutan yang akan menghasilkan sebuah fungsi baru.
Komposisi dua fungsi 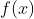 dan
dan 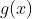 dinotasikan dengan simbol
dinotasikan dengan simbol  atau
atau  .
.
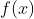 dan
dan 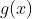 dinotasikan dengan simbol
dinotasikan dengan simbol  atau
atau  .
.
dimana


Sifat Komposisi Fungsi
Contoh :
diberikan fungsi :
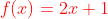


1.  = ….?
= ….?
 = ….?
= ….?
* fungsi 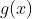 disubtitusikan ke fungsi
disubtitusikan ke fungsi 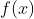
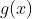 disubtitusikan ke fungsi
disubtitusikan ke fungsi 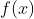

2. 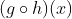 = ….?
= ….?
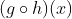 = ….?
= ….?
* fungsi  disubtitusikan ke fungsi
disubtitusikan ke fungsi 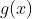
 disubtitusikan ke fungsi
disubtitusikan ke fungsi 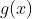

3. =…?
=…?
 =…?
=…?
* fungsi 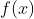 disubtitusikan terlebih dahulu ke fungsi
disubtitusikan terlebih dahulu ke fungsi 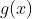 nah, hasilnya baru disubtitusikan ke fungsi
nah, hasilnya baru disubtitusikan ke fungsi  , perhatikan warna mewakili subtitusi ….ok!
, perhatikan warna mewakili subtitusi ….ok!
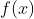 disubtitusikan terlebih dahulu ke fungsi
disubtitusikan terlebih dahulu ke fungsi 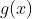 nah, hasilnya baru disubtitusikan ke fungsi
nah, hasilnya baru disubtitusikan ke fungsi  , perhatikan warna mewakili subtitusi ….ok!
, perhatikan warna mewakili subtitusi ….ok!
Bagaimana contoh diatas???sudah cukup jelas,kan???!!
Berhati-hatilah dalam mensubtitusikan ya….
Berhati-hatilah dalam mensubtitusikan ya….
Mencari salah satu fungsi jika komposisi fungsi diketahui
1. Mencari 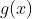 jika
jika 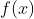 dan
dan  diketahui
diketahui
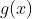 jika
jika 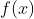 dan
dan  diketahui
diketahui
contoh soal dan pembahasan :
Diketahui  dan
dan  tentukan fungsi
tentukan fungsi  !
!
 dan
dan  tentukan fungsi
tentukan fungsi  !
!
jawab :

2. Mencari 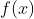 jika
jika 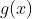 dan
dan  diketahui
diketahui
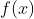 jika
jika 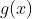 dan
dan  diketahui
diketahui
contoh soal dan pembahasan :
Diketahui 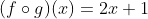 dan
dan  tentukan
tentukan  !
!
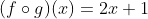 dan
dan  tentukan
tentukan  !
!
jawab :

Kita misalkan dulu :

Subtitusikan kembali ke fungsi :

BAB 4
TRIGONOMETRI
Pengukuran Sudut











Pengukuran Sudut

Berdasarkan gambar di atas dapat kita simpulkan bahwa pengukuran sudut merupakan salah satu aspek penting dalam pengukuran dan pemetaan kerangka maupun titik-titik detail.Sistem besaran sudut yang dipakai juga berbeda antara satu dengan yang lainnya. Sistem besaran sudut pada pengukuran dan pemetaan dapat terdiri dari:
- Sistem Besaran Sudut Seksagesimal
- Sistem Besaran Sudut Sentisimal
- Sistem Sesaran Sudut Radian
Dasar untuk mengukur besaran sudutnya seperti suatu lingkaran yang dibagi menjadi empat bagian, yang dinamakan kuadran yaitu Kudran I, II, III dan kuadran IV.
Untuk cara sexagesimal lingkaran dapat dibagi menjadi 360 bagian yang sama dan tiap bagiannya disebut derajat. Maka 1 kuadran dalam lingkaran tersebut = 900.
1o = 60’ 1’ = 60” 1o = 3600”
Perbandingan Trigonometri Pada Segitiga Siku – Siku

Untuk definisi perbandingan trigonometri sudut siku-siku pertama adalah:

Dan untuk definisi perbandingan trigonometri sudut siku-siku kedua, adalah:

Nilai Perbandingan Trigonometri Untuk Sudut – Sudut Istimewa
Nilai perbandingan memiliki beberapa tabel yang akan memudahkan kamu untuk menemukan hasilnya. Tabel itu sendiri memiliki 2 jenis tabel Istimewa. Ada apa saja? Yuk, perhatikan tabel di bawah ini:
Tabel perbandingan trigonometri sudut istimewa pertama

Tabel perbandingan trigonometri sudut istimewa kedua

Perbandingan Sudut dan Sudut Relasi Trinogometri I
Perbandingan sudut dan relasi trigonometri merupakan perluasan dari definisi dasar trigonometri tentang kesebangunan pada segitiga siku-siku yang hanya memenuhi sudut kuadran I dan sudut lancip (0 − 90°). Untuk contohnya kamu bisa perhatikan gambar di bawah ini ya!

Perbandingan Sudut dan Sudut Relasi Trigonometri II
Untuk setiap α lancip, maka (90° + α) dan (180° − α) akan menghasilkan sudut kuadran II. Dalam trigonometri, relasi sudut-sudut tersebut dinyatakan sebagai berikut:

Identitas Trigonometri
Identitas trigonometri adalah kesamaan yang memuat perbandingan trigonometri dari suatu sudut. Sebuah identitas trigonometri dapat ditunjukkan kebenarannya dengan tiga cara. Cara pertama, dimulai dengan menyederhanakan ruas kiri menggunakan identitas sebelumnya sampai menjadi bentuk yang sama dengan ruas kanan. Cara kedua, mengubah dan menyederhanakan ruas kanan sampai menjadi bentuk yang sama dengan ruas kiri. Cara ketiga, mengubah baik ruas kiri maupun ruas kanan ke dalam bentuk yang sama.
Ada beberapa rumus identitas trigonometri yang perlu kamu ketahui seperti:






Tidak ada komentar:
Posting Komentar